Constrained N-body Simulations
Download
Select a catalog and use the shell command to download it. Replace <API_KEY> with your API key.
Download with the command:
Download with the command:
Download with the command:
Data Overview
Background
The present-day density field of the flagship run is reconstructed from the observed galaxy distribution in the SDSS DR7 North Galactic Cap (NGC) sample within $z = [0.01, 0.12]$. The reconstruction volume is embedded into the simulation box, with randomly filled density fluctuations outside the reconstruction boundary.
Coordinate Systems
The simulation coordinate frame, defined by the simulation box, is related to the observational frame (J2000) by a translation and a rotation along the $z$-axis of the box. All data products of ELUCID (particles, groups, subhalos, etc.), unless explicitly specified, are in the simulation frame.
The translation vector, i.e., the location of the earth in the simulation box, is: $$ {\bf x}_{\rm 0} = (370, 370, 30)\, h^{-1} {\rm Mpc} $$ The rotation matrix is $$ {\bf R} = \begin{pmatrix} {\rm cos}(\phi_0) & {\rm sin}(\phi_0) & 0 \\ {\rm cos}(\phi_0 + \frac{\pi}{2}) & {\rm sin}(\phi_0 + \frac{\pi}{2}) & 0 \\ 0 & 0 & 1 \end{pmatrix} , $$ with a rotation angle $\phi_0 = 39^{\circ}$.
Given the simulation coordinate, ${\bf x}_{\rm sim}$, and velocity, ${\bf v}_{\rm sim}$, of any object, we can find its Cartesian coordinate, ${\bf x}_{\rm J2000}$, and velocity, ${\bf v}_{\rm J2000}$, in the J2000 frame by: $$ {\bf x}_{\rm J2000} = {\bf R} ({\bf x}_{\rm sim} - {\bf x}_{\rm 0}), $$ $$ {\bf v}_{\rm J2000} = {\bf R} {\bf v}_{\rm sim}. $$
Below are several well-known galaxies cluster, their tophat halo mass in the constrained simulation, their reconstructed coordinates in the simulation frame, and their observed J2000 coordinates:
| Cluster | mass $[10^{10}\,h^{-1}M_\odot]$ | ${\bf x}_{\rm sim}\,[h^{-1}{\rm Mpc}]$ | J2000 R.A, Dec. and $z_{\rm CMB}$ |
|---|---|---|---|
| Abell 1367 (Leo) | 36764.40 | (321.13, 335.49, 51.64) | 176.1231, 19.8390, 0.0208 |
| Abell 1656 (Coma) | 93658.61 | (332.63, 318.91, 63.53) | 194.9530, 27.9807, 0.0231 |
| Abell 1630 | 20159.47 | (254.91066 , 221.74059 , 44.49253) | 192.9357, 4.5617, 0.0636 |
| Abell 1564 | 19815.466796875 | (215.07, 198.16, 38.16) | 188.7393, 1.8413, 0.0792, 0.078 |
The spatial distribution of massive clusters in the local Universe and their progenitors resolved by the constrained simulation at several snapshots are shown below:
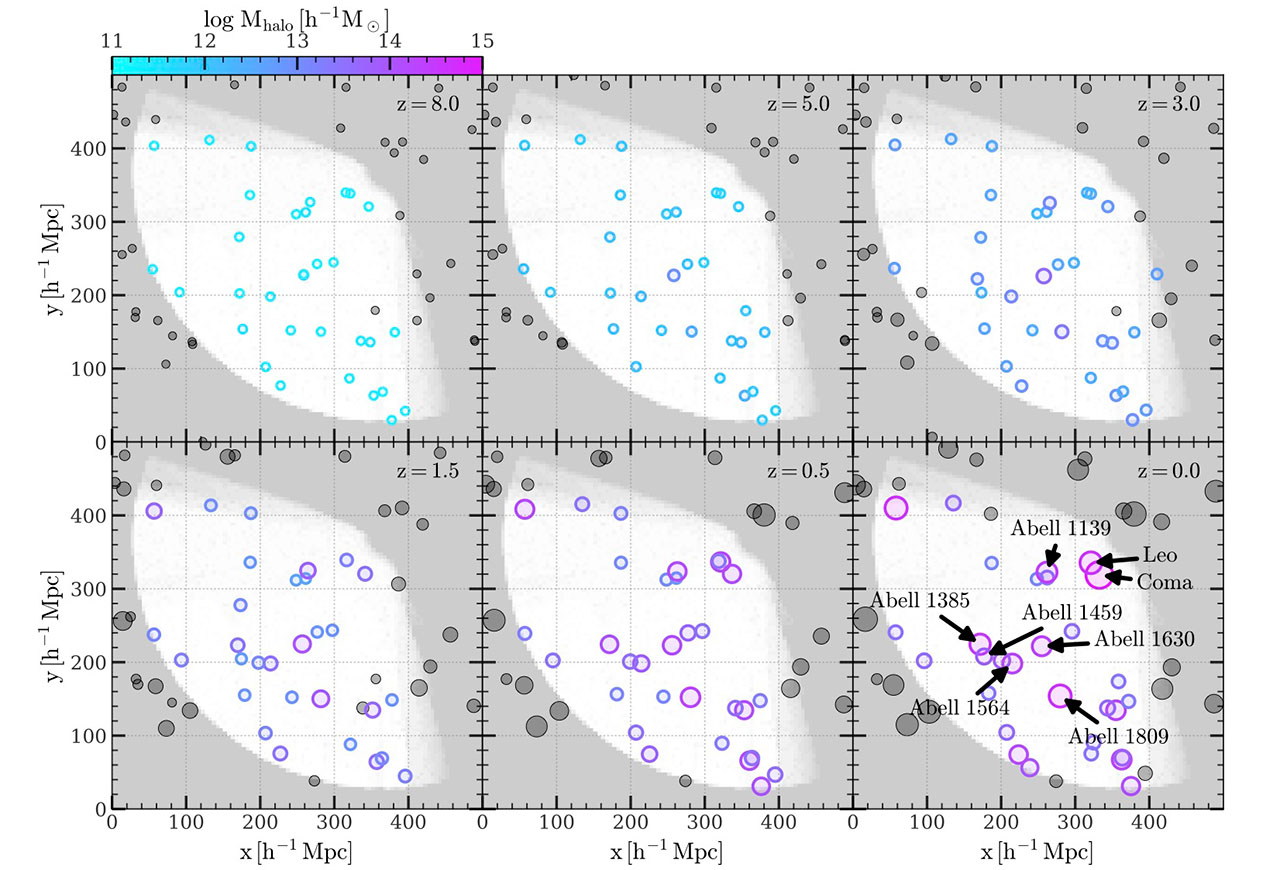
Masking the Reconstruction Volume
Since the reconstruction volume is only a part of the simulation box, we provide a 3D boolean array that can be used to mask-out the volume outside the reconstruction boundary. See Supplementary Catalogs for how to download and use it. The white region in each panel of above figure indicates the reconstruction volume.
The JSON File
We maintain a JSON-formatted file simulation.json for each simulation run. This is a light-weight, portable and human-readable file that keeps all the metainfo (simulation configurations, cosmological parameters, redshifts and times of dumps, etc.) of the run. It is designed:
- for a quick look of the simulation before actually downloading the binary files;
- as a portable way to extract or add simulation metainfo with minimal library dependency.
The Root Binary File
For each simulation run, we also maintain a root binary file simulation.hdf5. This serves as an "all-in-one" interface to all the data related to the run (simulation parameters, particles, groups, subhalos, trees, etc.). We highly recommend the users to use only this file for data access.
The underlying data files are linked virtually to the root binary file. To access a certain piece of data, one must organize all the data files in a simulation root dir as following by keeping their relative paths:
simulation.json # the JSON file
simulation.hdf5 # the root binary file
output/
├── snapdir_{snap:03d}/snapshot_{snap:03d}.{chunk}.hdf5 # particles
├── groups_{snap:03d}/tab_{snap:03d}.{chunk}.hdf5 # groups
└── subhalos_{snap:03d}/tab_{snap:03d}.{chunk}.hdf5 # subhalos
postprocessing/
└── trees/ # merger trees
└── SubLink/tree.{chunk}.hdf5
supplementary/
├── extended_trees/ # extended merger trees
│ └── tree.{chunk}.hdf5
└── reconstruction_pipeline/ # reconstruction metainfo
└── geometry.hdf5Note that it is not necessary to download all the data files. For example, if one only needs the particle data in several chunks at a snapshot, then only download those chunks. Visiting other data file that are not downloaded will raise an exception. We also note that the supplementary data are not linked to the root binary file because new catalogs will be gradually added.
Simulation Parameters
Numerical and cosmological parameters of the flagship run (ELUCID-DMOL0500N3072) are listed below. Note that the last two snapshots (snap=99, 100) are overlapped and the number of snapshots in use is 100.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ${\rm N_{snapshot}}$ | 101 | ${\rm N_{chunks}}$ | 2048 |
| ${\rm L_{box}}$ | $500.0 h^{-1}\, {\rm Mpc}$ | Number of space-filling cells ${\rm N_{cell, all}}$ | 16777216 |
| ${\rm N_{p, all}}$ | 28991029248 | $m_{\rm p}$ | $0.03087502 \times 10^{10} h^{-1}\,M_\odot$ |
| $h$ | 0.72 | $\Omega_{M,0}$ | 0.258 |
| $\Omega_{\Lambda,0}$ | 0.742 | ${\rm N_{bit\ mask\ pid}}$ | 36 |
| Gravitational softening length $\epsilon_{DM}$ | $3.5\ h^{-1}{\rm ckpc}$ |
Redshifts of Output Snapshots
| Snapshot | $z$ | Snapshot | $z$ | Snapshot | $z$ | Snapshot | $z$ | Snapshot | $z$ |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 18.409561 | 20 | 9.661436 | 40 | 4.856104 | 60 | 2.216634 | 80 | 0.766834 |
| 1 | 17.837003 | 21 | 9.346719 | 41 | 4.683271 | 61 | 2.121703 | 81 | 0.714689 |
| 2 | 17.280867 | 22 | 9.041370 | 42 | 4.515537 | 62 | 2.029569 | 82 | 0.664085 |
| 3 | 16.741506 | 23 | 8.745069 | 43 | 4.352746 | 63 | 1.940156 | 83 | 0.614971 |
| 4 | 16.217927 | 24 | 8.457427 | 44 | 4.194778 | 64 | 1.853385 | 84 | 0.567310 |
| 5 | 15.709555 | 25 | 8.178270 | 45 | 4.041466 | 65 | 1.769170 | 85 | 0.521054 |
| 6 | 15.216655 | 26 | 7.907416 | 46 | 3.892679 | 66 | 1.687450 | 86 | 0.476161 |
| 7 | 14.737870 | 27 | 7.644537 | 47 | 3.748270 | 67 | 1.608133 | 87 | 0.432595 |
| 8 | 14.273472 | 28 | 7.389403 | 48 | 3.608146 | 68 | 1.531159 | 88 | 0.390316 |
| 9 | 13.822720 | 29 | 7.141798 | 49 | 3.472132 | 69 | 1.456453 | 89 | 0.349284 |
| 10 | 13.385178 | 30 | 6.901516 | 50 | 3.340146 | 70 | 1.383961 | 90 | 0.309461 |
| 11 | 12.960631 | 31 | 6.668300 | 51 | 3.212051 | 71 | 1.313599 | 91 | 0.270816 |
| 12 | 12.548667 | 32 | 6.442027 | 52 | 3.087756 | 72 | 1.245319 | 92 | 0.233310 |
| 13 | 12.148725 | 33 | 6.222355 | 53 | 2.967105 | 73 | 1.179053 | 93 | 0.196911 |
| 14 | 11.760799 | 34 | 6.009231 | 54 | 2.850019 | 74 | 1.114742 | 94 | 0.161586 |
| 15 | 11.384054 | 35 | 5.802351 | 55 | 2.736404 | 75 | 1.052330 | 95 | 0.127304 |
| 16 | 11.018653 | 36 | 5.601575 | 56 | 2.626131 | 76 | 0.991758 | 96 | 0.094034 |
| 17 | 10.663984 | 37 | 5.406766 | 57 | 2.519107 | 77 | 0.932976 | 97 | 0.061746 |
| 18 | 10.319644 | 38 | 5.217668 | 58 | 2.415254 | 78 | 0.875930 | 98 | 0.030411 |
| 19 | 9.985631 | 39 | 5.034165 | 59 | 2.314452 | 79 | 0.820565 | 99 | 0.000000 |
Particle Catalog
Particles
| Dataset | Datatype, Shape Unit | Description |
|---|---|---|
| Coordinates | float32, (${\rm N_{p}}$,3) $h^{-1}{\rm Mpc}$ |
Comoving spatial coordinate in the periodic simulation box. The values may be slightly outside the box boundary [0, $L_{\rm box}$). |
| Velocities | float32, (${\rm N_{p}}$,3) $\sqrt{a}\, {\rm km/s}$ |
Spatial velocity. Multiply this value by $\sqrt{a}$ to obtain the peculiar velocity. |
| ParticleIDs | int64, ${\rm N_{p}}$ | Unique ID of this particle (referred to as pid, ranging from 0 to ${\rm N_{p, all}}-1$). Preserved across snapshots. |
Space-Filling Cells
To facilitate space-based data query, particle are ordered by their Peano-Hilbert space-filling cell index, as described by Springel et al. 2005 in the implementation detail of Gadget-2.
Briefly, ${\rm N_{cell, all}}$ cells are defined by the Peano-Hilbert space-filling curve (globally indexed by cell_id, ranging 0 from ${\rm N_{cell, all}}-1$), and each cell contains a subset of particles. In our data products of particles, cells are distributed into chunks so that each chunk contains a contiguous subset of cells. The hash table data group in each chunk contains the following datasets/attributes that describe layout of cells and particles in this chunk.
| Dataset/Attribute | Datatype, Shape Unit | Description |
|---|---|---|
| FirstCellID | int32, scalar | cell_id of the first cell in this chunk. |
| LastCellID | int32, scalar | cell_id of the last cell in this chunk. |
| ParticleOffsetsInCell | int32, ${\rm N_{cell}}$ | Offset (in all particles in this chunk) of the first particle of each cell in this chunk. |
Group and Subhalo Catalog
Groups
The group catalog stores the output of FoF algorithm, i.e., which subset of particles are linked to each FoF group and the IDs of those linked particles. The combination of group catalog and particle catalog allows extracting particles associated with each FoF group.
Groups at a given snap are stored as ${\rm N_{chunks}}$ chunks. Each chunk keeps a distinct set of groups and any group cannot spread across multiple chunks. However, the particles of groups in a chunk may be distributed into multiple chunks of the particle catalog.
To save memory, the field group_pid described below are bitwise Or-ing of cell_id and pid of each member particle by group_pid=(cell_id<<n_bit_mask_pid)|pid. The same applies to the field subhalo_pid field of subhalos.
| Dataset | Datatype, Shape Unit | Description |
|---|---|---|
| GroupLen | int32, ${\rm N_{group}}$ | Number of particles associated with each FoF group. |
| GroupOff | int32, ${\rm N_{group}}$ | The offset (i.e., index to group_pid) of the first particle in each FoF group. |
| GroupParticleIDs | int64, ${\rm N_{p\ in\ groups}}$ | cell_id and pid of each particle (bitwise OR-ed, referred to as group_pid). |
Subhalos
The subhalo catalog stores the output of the Subfind algorithm, i.e., the subhalo memberships of each group, and the particle memberships of each subhalo. In addition, several group properties, such as virial radius and mass, and subhalo properties, such as position and velocity, are also provided.
Like groups, subhalos at a given snap are distributed over chunks that are one-to-one corresponding to the chunks of groups.
| Dataset | Datatype, Shape Unit | Description |
|---|---|---|
| FirstSubOfGroup | int32, ${\rm N_{group} }$ | The index of first subhalo of each group in the same chunk. |
| NumSubPerGroup | int32, ${\rm N_{group} }$ | The Number of subhalos of each group in the same chunk. |
| SubOff | int32, ${\rm N_{subhalo} }$ | The index into subhalo_pid of the first particle of each subhalo. |
| SubLen | int32, ${\rm N_{subhalo} }$ | Number of particles associated with each subhalo. |
| SubParentHalo | int32, ${\rm N_{subhalo} }$ | The index (into group catalog in the same chunk) of the host group of each subhalo. |
| SubMostBoundID | int64, ${\rm N_{subhalo} }$ | The particle ID of the most bound particle of each subhalo (no bit-mask is needed). |
| ParticleIDs | int64, ${\rm N_{p\ in\ subhalos} }$ | cell_id and pid of each particle (bitwise OR-ed, referred to as subhalo_pid). |
Other datasets not listed here are Halo_M_Crit200, Halo_M_Mean200, Halo_M_TopHat200, Halo_R_Crit200, Halo_R_Mean200, Halo_R_TopHat200, SubHalfMass, SubPos, SubSpin, SubVel, SubVelDisp, and SubVmax. See the merger tree catalog below for their detailed meanings.
Merger Tree Catalog
SubLink Trees
Subhalos in ELUCID are linked by the SubLink algorithm across different redshifts. Linked subhalos form subhalo merger trees which describe the assembly histories of subhalos on the tree.
SubLink trees are represented in memory by a contiguous array of Subfind subhalos. Progenitor/descendant relationships are described the indexing fields of subhalos. For any subhalo h, we have the following fields:
- FirstProgenitor: index of the most massive progenitor subhalo of h.
- NextProgenitor: index of the next most massive progenitor which shares the same descendant as h.
- Descendant: index of the descendant subhalo of h.
For convenience, two additional indices are provided to link subhalos in the same FoF group:
- FirstHaloInFOFgroup: index of the central subhalo (i.e., most massive subhalo, as calculated by sum of linked dark matter particles) of the FoF group that hosts h. A central subhalo has FirstHaloInFOFgroup pointing to itself.
- NextHaloInFOFgroup: index of the subhalo in the same FoF group and next massive to h.
Subhalos connected by any of the above five indices are considered in the same "tree" and stored contiguously. Trees are distributed in ${\rm N_{chunks}}$ chunks. Each chunk contains trees one after another. A tree cannot distributed in more than one chunk. All the five indices are 0-based and started from the first subhalo in each tree. All of them, except FirstHaloInFOFgroup, can be -1, indicating none of such link exists. Note that the FirstProgenitor and Descendant may skip at most one snapshot for taking temporarily unresolved subhalos into account.
| Dataset | Datatype, Shape Unit | Description |
|---|---|---|
| FirstProgenitor | int32, ${\rm N_{subhalo\ in\ trees}}$ | Index of the most massive progenitor subhalo. |
| NextProgenitor | int32, ${\rm N_{subhalo\ in\ trees}}$ | Index of the next most massive progenitor subhalo that shares the same descendant. |
| Descendant | int32, ${\rm N_{subhalo\ in\ trees}}$ | Index of the descendant subhalo. |
| FirstHaloInFOFgroup | int32, ${\rm N_{subhalo\ in\ trees}}$ | Index of the most massive subhalo in the same FoF group. |
| NextHaloInFOFgroup | int32, ${\rm N_{subhalo\ in\ trees}}$ | Index of the next most massive subhalo in the same FoF group. |
| Pos | float32, (${\rm N_{subhalo\ in\ trees}}$, 3) $h^{-1}\,{\rm Mpc}$ | Comoving spatial position in the periodic box, defined as the position of its most bound particle. may be slightly out of $[0, L_{\rm box})$. |
| Vel | float32, (${\rm N_{subhalo\ in\ trees}}$, 3) $\rm km/s$ | Peculiar velocity of the subhalo, defined as the averaged velocities of all particles linked to it, with a $\sqrt{a}$ multiplied. |
| M_Mean200 | float32, ${\rm N_{subhalo\ in\ trees}}$ $10^{10}\,h^{-1}M_\odot$ | Total mass of the FoF group enclosed in a sphere whose mean density is 200 times the mean density of the Universe of that time. This field is only significant for a central subhalo and set to 0 for a satellite subhalo. |
| M_Crit200 | float32, ${\rm N_{subhalo\ in\ trees}}$ $10^{10}\,h^{-1}M_\odot$ | Total mass of the FoF group enclosed in a sphere whose mean density is 200 times the critical density of the Universe of that time. This field is only significant for a central subhalo and set to 0 for a satellite subhalo. |
| M_TopHat | float32, ${\rm N_{subhalo\ in\ trees}}$ $10^{10}\,h^{-1}M_\odot$ | Total mass of the FoF group enclosed in a sphere whose mean density is $\Delta_c$ times the critical density of the Universe of that time, according to the spherical collapse model of Bryan+1998. This field is only significant for a central subhalo and set to 0 for a satellite subhalo. |
| Vmax | float32, ${\rm N_{subhalo\ in\ trees}}$ $\rm km/s$ | Maximal value of the circular velocity, $\sqrt{\frac{G M_{< r}}{r}}$, where $r$ is the physical distance to the minimal potential of the subhalo, $M_{< r}$ is the total mass enclosed in a sphere of radius $r$. Only particles linked to this subhalo by Subfind are included in the computation. |
| Len | int32, ${\rm N_{subhalo\ in\ trees}}$ | Number of particles linked to this subhalo. |
| Spin | float32, (${\rm N_{subhalo\ in\ trees}}$, 3) $h^{-1}{\rm Mpc\,km/s}$ | Averaged physical specific angular momentum of particles per axis, computed as the average of relative position vector cross relative velocity vector of all linked particles. Position and velocity vectors are computed relative to the central of mass of the subhalo, both are physical values. |
| VelDisp | float32, ${\rm N_{subhalo\ in\ trees}}$ $\rm km/s$ | 1-D physical velocity dispersion of all linked particles (i.e., 3-D dispersion divided by $\sqrt{3}$). Hubble flow is included. |
| SubhalfMass | float32, ${\rm N_{subhalo\ in\ trees}}$ $h^{-1}\,{\rm Mpc}$ | Physical radius (relative to the minimal potential) that encloses half of the bound mass of the subhalo. |
| SnapNum | int32, ${\rm N_{subhalo\ in\ trees}}$ | Snapshot number of this subhalo. |
| FileNr | int32, ${\rm N_{subhalo\ in\ trees}}$ | The chunk in subhalo catalog that stores this subhalo. |
| SubhaloIndex | int32, ${\rm N_{subhalo\ in\ trees}}$ | The index of subhalo in the chunk of subhalo catalog. |
| MostBoundID | int64, ${\rm N_{subhalo\ in\ trees}}$ | pid of the most bound particle linked to this subhalo. |
Code Samples
ELUCID data products, besides of JSON meta files, are stored in HDF5 format. The HDF group officially provide C/C++, Python, Fortran application program interfaces (APIs) and command line interface (CLI) to manipulate and access HDF5 files. In the below, we demonstrate a few examples of how to access ELUCID data using these tools.
Using "simulation.json"
The JSON file is just a human-readable and editable plain text file. The easiest way is to use a code editor, such as vim, VSCode, etc., to open, read and edit it.
To use it in a programming language, find a JSON parser for that language and parse the file content into objects in the language. For example, in Python, we can use the built-in "json" module:
import json
with open('simulation.json', 'r') as f:
sim_meta = json.load(f)
sim_metaOutput:{
'formal_name': 'ELUCID-DMOL0500N3072',
'simulation_definition': {
'cosmology': { 'name': 'WMAP5', 'hubble': 0.72, 'omega_m0': 0.258, ...},
'is_baryon': False,
'n_snapshots': 101, 'mass_table': [0.0, 0.03087502, 0.0, 0.0, 0.0, 0.0],
'box_size': 500.0, ...
}, ...
}
The parsed "sim_meta" is just an ordinary Python "dict". We can, for example, get the cosmological parameters as:
sim_meta['simulation_definition']['cosmology']Output:{'name': 'WMAP5', 'hubble': 0.72,
'omega_m0': 0.258, 'omega_l0': 0.742, 'omega_b0': 0.044,
'sigma_8': 0.8, 'n_spec': 0.96, 't_cmb': 2.725}
Navigating Data on Shell
To have a quick look of the data, use h5ls command that comes with HDF5 installation to list the data group and datasets in the simulation root file "simulation.hdf5":
$ h5ls simulation.hdf5Header Group
Snapshots Group
Trees GroupTo look at all data groups and datasets below a certain level, use the recursive option "-r", and a "/" separarated path followed by the file name to specify the target data group. For example, to see the data groups and datasets in the first chunk of the SubLink trees, type:
$ h5ls -r simulation.hdf5/Trees/SubLink/0/Header Group
/Header/HaloOffsetInTree Dataset {18326}
/Header/NumHalosInTree Dataset {18326}
/Subhalos Group
/Subhalos/Descendant Dataset {1715555}
/Subhalos/FileNr Dataset {1715555}
/Subhalos/FirstHaloInFOFgroup Dataset {1715555}
/Subhalos/FirstProgenitor Dataset {1715555}
...To see the detail contents of datasets or attributes, use h5dump command. The -a option allows printing the attribute in detail:
$ h5dump -a /Header/HubbleParam simulation.hdf5HDF5 "simulation.hdf5" {
ATTRIBUTE "HubbleParam" {
DATATYPE H5T_IEEE_F64LE
DATASPACE SCALAR
DATA {
(0): 0.72
}
}
}Here, we know that the Hubble parameter is 0.72, stored as a double-precision floating-point scalar value.
To see a slice of a dataset, use -d option followed by the dataset path, -s to specify the starting indices of the dataset array at every dimension, -c to specify the number of elements to print at every dimension. For example, to see the first 5 particles' coordinates in the first chunk of snapshot 76, type:
$ h5dump -d /Snapshots/76/0/PartType1/Coordinates -s '0,0' -c '5,3' simulation.hdf5HDF5 "simulation.hdf5" {
DATASET "/Snapshots/76/0/PartType1/Coordinates" {
DATATYPE H5T_IEEE_F32LE
DATASPACE SIMPLE { ( 13158492, 3 ) / ( 13158492, 3 ) }
SUBSET {
START ( 0, 0 );
STRIDE ( 1, 1 );
COUNT ( 5, 3 );
BLOCK ( 1, 1 );
DATA {
(0,0): 0.237073, 0.426335, 0.282894,
(1,0): 0.203004, 0.295625, 0.302116,
(2,0): 0.181315, 0.068548, 0.251428,
(3,0): 0.165277, 0.1137, 0.737562,
(4,0): 0.146942, 0.280833, 0.743508
}
}
}
}Python
To work with ELUCID data in Python, use "h5py" to load all data from the root file "simulation.hdf5". In this tutorial, we also use several other packages. Import all of them by:
import h5py
import pandas as pd
import numpy as npNow we open the root file and see the available data groups under it:
file = h5py.File('simulation.hdf5', 'r')
file.keys()Output:<KeysViewHDF5 ['Header', 'Snapshots', 'Trees']>
The three data groups "Header", "Snapshots" and "Trees" store the simulation parameters, snapshots and merger trees, respectively.
Loading Simulation Parameters
To see the available simulation parameters, open "Header" and call its "keys()" method. Small-size parameters are compactly kept as the attribute and can be accessed via "attrs":
header = file['Header']
header.keys(), header.attrs.keys()Output:(<KeysViewHDF5 ['Redshifts', 'SnapNums', 'Times']>,
<KeysViewHDF5 ['BoxSize', 'FlagCooling', ...)
For example, to look at the redshifts of snapshots, write:
header['Redshifts'][()]Output:array([ 1.8409561e+01, 1.7837003e+01, 1.7280867e+01, 1.6741506e+01,
..., 3.0410522e-02, -2.2204460e-16, -2.2204460e-16])
To get the Hubble parameter $h$, the total number of particles at every snapshot, and the masses of particles (of type 1, i.e., dark matter), write:
header.attrs['HubbleParam'], header.attrs['NumPart_Total'][1], header.attrs['MassTable'][1]Output:(0.72, 28991029248, 0.030875024131732435)
Loading Particles
To load particle in the first chunk (chunk_id = 0) of snapshot 76, write:
snap_data = file['Snapshots/76']
chunk = snap_data['0']
chunk.keys()Output:<KeysViewHDF5 ['FoFTable', 'HashTableType1', 'PartType1', 'SubfindTable']>
The data groups "FoFTable" and "SubfindTable" store FoF halo and Subfind subhalo catalogs, respectively; "PartType1" keeps particles; "HashTableType1" stores the indices of space-filling cells of this chunk.
We can look at the available properties of particles, and load, for example, the positions of the first 10 particles by:
ps = chunk['PartType1']
ps.keys(), ps['Coordinates'][:10]Output:(<KeysViewHDF5 ['Coordinates', 'ParticleIDs', 'Velocities']>,
array([[0.2370728 , 0.4263347 , 0.282894 ], ..., [0.6061265 , 0.39591527, 0.58704 ]], dtype=float32))
Because particles are stored as cells, it is an usual task to load particles in a given cell. To do this, we first need to know the cell indices of each chunk. This is done by accessing the attributes "FirstCellID" and "LastCellID" in the hash table, by:
cells = chunk['HashTableType1']
cells.attrs['FirstCellID'], cells.attrs['LastCellID']Output:(0, 8191)
It is seen that this chunk stores the particles in the first 8192 cells. To load all particles in a single cell, we retrieve the offset range of particles in the target cell, and use it to load particles. For example, the following code sample loads the velocities of the first cell in this chunk:
b, e = cells['ParticleOffsetsInCell'][:2]
ps['Velocities'][b:e] Output:array([[-32.977104, 673.516 , 702.3557 ],
...,
[-43.265377, 681.66113 , 786.0533 ]], dtype=float32)
Loading Groups and Subhalos
The group catalog stores particles indices (pid) and cell indices (cell_id) of particles belonging to each group. Use load them, open the "FoFTable" of a chunk and view its available attributes and datasets by:
fof = chunk['FoFTable']
fof.attrs.keys(), fof.keys()Output:(<KeysViewHDF5 ['NumGroup_ThisFile', 'NumPart_ThisFile']>,
<KeysViewHDF5 ['GroupLen', 'GroupOff', 'GroupParticleIDs']>)
To get particle and cell indices of a group, take "GroupOff" and "GroupLen" and use them to slice "GroupParticleIDs". For example, the following code sample loads "GroupParticleIDs" of the first group in this chunk:
off, n_p = fof['GroupOff'][0], fof['GroupLen'][0]
group_pids = fof['GroupParticleIDs'][off:off+n_p]The loaded group_pids is bitwise OR-ing of pid and cell_id. To separate them, we need to know the number of shifted bits, which can be retrieved from the attribute "GroupTableMaskNumBit" of the header:
n_bit_mask_pid = header.attrs['GroupTableMaskNumBit']
cell_ids = group_pids >> n_bit_mask_pid
pids = group_pids & ((1 << n_bit_mask_pid) - 1)
cell_ids, pidsOutput:(array([1414, 1414, 1414, ..., 1461, 1461, 1461]),
array([1604886561, 1746499660, 1831504915, ..., 2020184116, 2020187230,
2048504924]))
Particles in a group may belong to multiple nearby cells which may belong to multiple chunks. To load particles of the group, we first build a map from cell indices to chunk indices, and then use this map to get the chunk indices that contain the particles of the group. This can be done by:
n_chunks = header.attrs['NumFilesPerSnapshot']
n_cells = header.attrs['HashTableSize']
cell2chunk = np.empty(n_cells, dtype=int)
for i_c in range(n_chunks):
chunk = snap_data[str(i_c)]
cells = chunk['HashTableType1']
b, e = cells.attrs['FirstCellID'], cells.attrs['LastCellID']
cell2chunk[b:e] = i_c
cell_ids = np.unique(cell_ids)
chunk_ids = cell2chunk[cell_ids]Now we have the chunk indices that contain the particles of the group. To load the particles, we iterate over the chunks and load the particles in the target cells. For example, the following code sample loads the positions of the particles in the group and computs the center of mass of the group:
pids = pd.Index(pids)
xs = []
for chunk_id, cell_id in zip(chunk_ids, cell_ids):
chunk = snap_data[str(chunk_id)]
ps, cells = chunk['PartType1'], chunk['HashTableType1']
_pids, _xs = ps['ParticleIDs'], ps['Coordinates']
p_offs = cells['ParticleOffsetsInCell']
n_cells, n_ps = len(p_offs), len(_pids)
cell_off = cell_id - cells.attrs['FirstCellID']
b = p_offs[cell_off]
e = p_offs[cell_off+1] if cell_off + 1 < n_cells else n_ps
filter = pids.get_indexer(_pids[b:e]) >= 0
xs.append(_xs[b:e][filter])
xs = np.concatenate(xs)
x_com = xs.mean(0)
print(f'{len(xs)} particles found, center of mass: {x_com}')Output:305341 particles found, center of mass: [29.704235 28.84837 4.2054057]
Altough we have many cells in each chunk, for a small sample of groups, only a small number of cells are needed to be loaded. Depending on the target group sample in specific application, the loading algorithm should be tuned if IO performance is critical.
Similarly, we can load subhalo catalog from the "SubfindTable" data group of each chunk. For example, the following code sample opens the data group of the first chunk and prints the number of groups, subhalos, and particles linked to subhalos:
chunk = snap_data['0']
subfind = chunk['SubfindTable']
subfind.attrs['NumGroup_ThisFile'], subfind.attrs['NumSub_ThisFile'], subfind.attrs['NumPart_ThisFile']Output:(24873, 25500, 7440527)
To find information of all subhalos in a given group, load the offset of the first subhalo and the number of subhalos in the group, and use them to slice the subhalo properties. For example, we load the maximal circular velocities of subhalos in the 9th group of this chunk by:
grp_id = 9
first_sub = subfind['FirstSubOfGroup'][grp_id]
n_subs = subfind['NumSubPerGroup'][grp_id]
subfind['SubVmax'][first_sub:first_sub+n_subs]Output:array([291.05557 , 353.88458 , 231.2501 , 186.4264 , 164.374 ,
133.07835 , 117.472244, 141.52196 , 113.723656, 139.05486 , ...])
To find particles in a subhalo, load the offset of the first particle and the number of particles in the subhalo, and use them to slice indices array. For example, we load subhalo_pid of the first subhalo in the above group by:
off, n_p = subfind['SubOff'][first_sub], subfind['SubLen'][first_sub]
subhalo_pids = subfind['ParticleIDs'][off:off+n_p]Output:array([75180079984635, 75180098859016, 75180061119494, ...,
75179881763842, 75179957374951, 75179872320523])
Loading Subhalo Merger Trees
SubLink trees are stored under "Trees/SubLink" data group and also distributed over chunks. For example, we open the first chunk and look at the available header attributes and datasets, and available subhalos properties by:
chunk = file['Trees/SubLink/0']
header, subs = chunk['Header'], chunk['Subhalos']
header.keys(), header.attrs.keys(), subs.keys()Output:(<KeysViewHDF5 ['HaloOffsetInTree', 'NumHalosInTree']>,
<KeysViewHDF5 ['NumHalos', 'NumTrees']>,
<KeysViewHDF5 ['Descendant', 'FileNr', 'FirstHaloInFOFgroup', ...]>)
Subhalos in a tree is stored contiguous. In the following code sample, we load subhalo properties in the first tree. This is done by first retrieving the offset and number of subhalos in the tree, and then slicing the "FirstProgenitor", "M_TopHat", and "SnapNum" datasets:
off, n_sub = header['HaloOffsetInTree'][0], header['NumHalosInTree'][0]
f_pros = subs['FirstProgenitor'][off:off+n_sub]
masses = subs['M_TopHat'][off:off+n_sub]
snaps = subs['SnapNum'][off:off+n_sub]With these properties loaded, we can find the half mass formation snapshot of any central subhalo in the tree. For example, the first subhalo's approximate formation snapshot can be found by recursively following the "FirstProgenitor" property until the mass is less than the given threshold:
id = 0
root_mass = masses[id]
while id >= 0:
f_pro, mass, snap = f_pros[id], masses[id], snaps[id]
if mass > 1.0e-5 and mass < 0.5 * root_mass:
break
id = f_pro
print(f'Half mass formation snapshot: {snap}')
Output:Half mass formation snapshot: 89
C++
The official C/C++ bindings provided by the HDF group is a little bit verbose for demonstration. In the below, we use the C++ HPC toolkit HIPP to show how to load ELUCID datasets. It is functionally equivalent to the official bindings, with much more elegant API and negligible overhead owing to the metaprogramming facilities of C++.
The usual usage of HIPP is demonstrated in the following code sample:
#include <hipp/io.h>
using namespace std;
namespace h5 = hipp::io::h5; // the HDF5 IO module of HIPP
using hipp::pout; // an output stream for pretty printing
int main(int argc, char const *argv[]) {
h5::File file("simulation.hdf5", "r");
// use "file" to load ELUCID data ...
return 0;
}Here, we include the header file of the IO module provided by HIPP. We alias the namespace h5 for a shortcut. We also expose the pout object for pretty printing in this tutorial. In the main function, we open a HDF5 file by creating an h5::File object with read-only mode. Then, we can load all data from this single file instance.
The compilation and execution command are like the following, supposing all the shell environmental variables (CPLUS_INCLUDE_PATH, LIBRARY_PATH and LD_LIBRARY_PATH, if using gcc-compatible compiler) are exported according to the installation manual of HIPP.
g++ -std=c++20 -O3 -Wall src.cpp -lhipp_io -lhipp_core -lhdf5 && ./a.outauto header = file.open_group("Header");
auto hubble = header.attrs().get<double>("HubbleParam"),
omega_m0 = header.attrs().get<double>("Omega0");
auto redshifts = header.datasets().get<vector<double> >("Redshifts");
pout << "hubble=", hubble, ", omega_m0=", omega_m0, '\n',
"redshifts=", redshifts, endl;Output:hubble=0.72, omega_m0=0.258
redshifts=<vector> {18.4096, 17.837, ..., 0.0304105, -2.22045e-16, -2.22045e-16}Here, the methods attrs() and datasets() returns proxy objects that can be used to load attributes and datasets, respectively. The get<T>() method of a proxy object loads the data into a variable typed T and return it. The pout object followed by a << operator and multiple comas streams object into stdout.
Loading Particles
To load particles, open the data group of given snapshot and chunk index, and load the particle number and positions by:
auto ps = file.open_group("Snapshots/76/0/PartType1");
auto n_ps = ps.attrs().get<int>("NumPart_ThisFile");
auto xs = ps.datasets().get<vector<std::array<float, 3> > >("Coordinates");
pout << "Number of particles=", n_ps, endl;
pout << "First 5 positions:\n";
for(int i=0; i<5; ++i){
pout << xs.at(i), endl;
}Output:Number of particles=13158492
First 5 positions:
<array> {0.237073, 0.426335, 0.282894}
<array> {0.203004, 0.295625, 0.302116}
<array> {0.181315, 0.068548, 0.251428}
<array> {0.165277, 0.1137, 0.737562}
<array> {0.146942, 0.280833, 0.743508}Loading Subhalo Merger Trees
ELUCID trees are organized as contiguous array of subhalos. In C++, properties of a subhalo is often represented by a struct for compact algorithm implementation and efficient memory access. For example, we define the following Subhalo type:
struct Subhalo {
float M_TopHat;
float Pos[3];
int FirstProgenitor, Descendant, FirstHaloInFOFgroup, NextHaloInFOFgroup;
int SnapNum;
};To load trees in a chunk, we open the data group and use the "Header" to get the offset and length of each tree. This can be done by:
auto tree_cat = file.open_group("Trees/SubLink/0");
auto header = tree_cat.open_group("Header");
auto offs = header.datasets().get<vector<int> >("HaloOffsetInTree"),
lens = header.datasets().get<vector<int> >("NumHalosInTree");Then, we use the HIPP_IO_H5_XTABLE_DEF macro to define a data loader for subhalos and load all subhalos in trees of the chunk:
HIPP_IO_H5_XTABLE_DEF(loader, Subhalo,
M_TopHat, Pos, FirstProgenitor, Descendant,
FirstHaloInFOFgroup, NextHaloInFOFgroup, SnapNum);
auto all_subs = loader.read(tree_cat.open_group("Subhalos"));Note that the first two parameters of the macro is the desired variable identifier and the struct type name, and the following parameters are field names of the struct in arbitrary order. We can print the number of trees and subhalos in the chunk by:
int n_trees = offs.size(), n_subs = all_subs.size();
pout << n_trees, " trees and ", n_subs, " subhalos found in the chunk\n";Output:18326 trees and 1715555 subhalos found in the chunkTo access subhalo in a specific tree, we take its offset and length, and use them to index into the subhalo array. For example, in the following code sample, we traverse all subhalos in the fourth tree and find a "root" subhalo (i.e., subhalo without descendant):
int off = offs.at(3), len = lens.at(3), root_id {};
Subhalo *subs = &all_subs.at(off);
for(int i=0; i<len; ++i){
auto &sub = subs[i];
if( sub.Descendant == -1 ) {
root_id = i; break;
}
}
auto root = subs[root_id];
pout << "Root subhalo: index=", root_id,
", mass=", root.M_TopHat,
", snap=", root.SnapNum,
", position=", root.Pos, endl;Output:Root subhalo: index=0, mass=4990.55, snap=100, position=0x7fffa7586584It is seen that the first subhalo in the tree is a root at snapshot 100 (z=0). We can also find the half mass formation snapshot of the root subhalo by traversing along the progenitor chain until the mass drops below half of the root:
int id = root_id;
while(id >= 0) {
auto &sub = subs[id];
if( sub.FirstHaloInFOFgroup == id
&& sub.M_TopHat < subs[root_id].M_TopHat * 0.5 )
{
pout << "Half mass formation snapshot: ", sub.SnapNum, endl;
break;
}
id = sub.FirstProgenitor;
}Output:Half mass formation snapshot: 94The "FirstHaloInFOFgroup" and "NextHaloInFOFgroup" fields are used to identify subhalos in the same FoF group. For example, for the root subhalo defined above, we can count the subhalos in the host group by:
int count = 0;
id = subs[root_id].FirstHaloInFOFgroup;
while(id >= 0) {
++ count;
id = subs[id].NextHaloInFOFgroup;
}
pout << count, " subhalos found in the FoF group\n";Output:103 subhalos found in the FoF group